

Leonardo Pisano detto il Fibonacci (1175-1250), cioè figlio di Bonaccio, individuò questa serie per la prima volta nel 1202, per risolvere un problema pratico: quante coppie di conigli si ottengono in un anno da una sola coppia supponendo che produca ogni mese (tranne il primo) una nuova coppia che a sua volta diventa fertile a partire dal secondo mese? La risposta è 144 coppie di conigli. In questa serie ogni numero è il risultato della somma dei due precedenti: 0, 1, 1, 2, 3, 5, 8, 13... fino all’infinito. Fino al XIX secolo a questa successione non fu attribuita alcuna importanza, finché si scoprì che può essere applicata, per esempio, nel calcolo delle probabilità, nella sezione aurea e nel triangolo aureo. I numeri di Fibonacci si trovano anche in natura, per esempio nella disposizione delle foglie (vedere disegno sopra). In molti alberi, scegliendo una foglia su uno stelo e assegnandole il numero “0”, contando il numero di foglie fino ad arrivare a una perfettamente allineata con la foglia “0”, probabilmente si troverà un numero di Fibonacci. Anche i petali di moltissimi fiori sono un numero di Fibonacci. Al matematico pisano si deve anche l’introduzione dei numeri arabi in Italia.
La sezione aurea o rapporto aureo o numero aureo di Fidia, chiamato anche proporzione divina, è un numero irrazionale che si ottiene effettuando il rapporto tra due lunghezze disuguali delle quali la maggiore misura, a, è medio proporzionale tra la misura minore, b, e la somma delle due (a+b). si indica con la lettera greca phi ed è rappresentato dalla seguente formula:
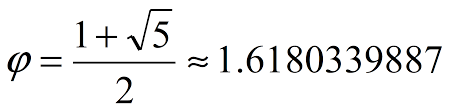
Partiamo dalla elaborazione di una successione numerica, individuata proprio da Leonardo Fibonacci nel 1202, che si rendeva funzionale alla risoluzione di un problema relativo alla evoluzione annuale della popolazione dei conigli: quante coppie di conigli si ottengono in un anno da una sola coppia di partenza, supponendo che essa produca ogni mese, ad eccezione del primo, una nuova coppia che, a sua volta prolifica a partire dal secondo mese?
La risposta è 144 coppie di conigli. In questa serie ogni numero è il risultato della somma dei due numeri precedenti: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144… andando così avanti all’infinito.
Facendo il rapporto tra due numeri consecutivi della serie di Fibonacci, tale rapporto approssima sempre meglio il numero aureo.